Темная сторона Вселенной

Теперь поговорим о более загадочных и менее изученных вещах — чёрных дырах. Все знают о черных дырах. Но откуда пришло это понятие?

Первый человек, который предположил существование таких компактных объектов с гигантским притяжением, был Джон Мичелл, английский естествоиспытатель. Геофизики его считают отцом-основателем геофизики, астрономы тоже его очень уважают.

Он первый подсчитал, что если тело будет достаточно массивным и компактным, то вторая космическая скорость на его поверхности может стать равной скорости света. И что тогда? Тогда с его поверхности не может стартовать даже свет, а все остальные тела во Вселенной (частицы и прочие), движутся медленнее света, то есть ничто не сможет покинуть поверхность такого объекта.

Мичелл опубликовал эту работу, но она как-то прошла не очень замеченной, потому что уж слишком маленьким получался радиус такого тела. Даже если взять массу Солнца, его размер должен быть около трех километров, но кто же поверит, что гигантская звезда может быть размером в три километра? Однако время шло, и другие ученые заинтересовались этой идеей, и знаменитый французский математик астроном Пьер Симон Лаплас открыл ее заново.

Сделал он это, не ссылаясь на работу Мичелла, а просто опубликовав под своим именем книгу. Может быть он действительно не читал ту работу, сам пришел к этой идее и опубликовал ее в довольно известной, можно сказать, научно-популярной, своей книге «Система мира».  Она тоже осталась незамеченной.

Книгу-то люди читали, но идея показалась настолько фантастической, что никто не обратил на нее внимание. И только в начале двадцатого века, когда новую теорию гравитации общей теории относительности создал Альберт Эйнштейн, идея о черных дырах возродилась уже на основе новой, гораздо более точной теории, чем теория тяготения Ньютона.

Теория Эйнштейна доказала свою состоятельность и используется физиками как рабочий инструмент. Посмотрите пожалуйста на уравнения Эйнштейна.

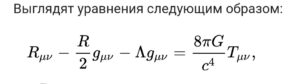
Выглядят они довольно просто: запись в одну строчку. Но не надо заблуждаться. Это тензорное уравнение, в нем целый набор довольно сложных уравнений, и решение их представляет собой большую проблему.

Первым, кто решил уравнения гравитационного поля, уравнения гравитации Эйнштейна, был немецкий астроном и математик, оптик, директор обсерватории Карл Шварцшильд.

Фигура легендарная. Он очень многое сделал для науки, и многие его идеи только сейчас начинают работать. Прожил он недолго. В 2014 году началась Первая мировая война. Почти всех мужчин Германии мобилизовали в окопы.

В окопах Шварцшильд заболел, заболел очень тяжело, и в госпитале через несколько дней умер. Но буквально накануне своей смерти опубликовал статью, где были решены уравнения Эйнштейна.

В чем же было его открытие? Оказалось, что если маленькое тело имеет большую массу, то вокруг него существуют две характерные сферы, два характерных расстояния.

Первое расстояние мы сегодня в космонавтике называем первая космическая скорость, скорость полета спутника вокруг Земли или вокруг другого небесного тела.

Какой спутник может летать по поверхности этой сферы? Частица света — фотон. Если рядом с компактным телом на небольшом расстоянии мы запустим лучи света, то изогнутый притяжением к этой массе свет будет путешествовать вокруг нее. Поэтому сфера называется фотонная.

А внутри нее находится еще более загадочная сфера, так называемый горизонт событий. Смысл его в том, что, падая издалека, любое тело может пересечь его и двигаться туда под действием притяжения этому компактному объекту.

Попав внутрь горизонта событий ни одно тело, и даже луч света, не может оттуда вырваться.

То есть смысл этого расстояния в том, что на нем вторая космическая скорость равна скорости света.

Удивительно, что решение в рамках общей теории относительности Эйнштейна в точности соответствовало ньютоновой гравитации. Это, конечно, совпадение, но оказалось, что та же самая формула выходит при решении общей теории относительности, точно такое же решение, которое любой школьник может получить, взяв вторую космическую скорость равной скорости света, и тогда масса этой частицы и расстояние от нее сферы горизонта событий точно будут даны этой формулой.

Совпадение удобное для тех, кто увлекается физикой.

Это решение было опубликовано, но и оно практически осталось незамеченным. Во-первых, потому что это были годы Первой мировой войны, а во-вторых, потому, что казалось, что это чистая математика и не стоит обращать на нее внимание.

Следующий шаг в математике, в решении уравнений Эйнштейна, сделал молодой математик Рой Кер. Он решил более сложное уравнение. Он решил уравнение не просто для маленькой компактной массы, а в том случае, если она еще и вращается вокруг своей оси.

Мы не видим ни одного космического объекта, который бы не вращался.

Вращение — это естественное состояние любого космического тела

Уравнение становится намного сложнее. Оказалось, что кроме горизонта событий, такая вращающаяся масса будет окружена еще и так называемым пределом статичности, а область между этими двумя поверхностями называют эргосферой.

В чем ее особенность? Взлетев внутрь предела событий в пределах статичности, но еще не пересекая поверхность горизонта событий, тело может оттуда ускользнуть.

Например, лучи света или быстро летящие частицы, могут проникнуть сюда и вылететь, но попав туда, тело не может оставаться в неподвижности.

Оно обязано вращаться в ту же сторону, куда вращается само массивное тело. Ситуация примерно такая, как если бы вы вскочили на вращающуюся карусель: вы встали на нее, и вам кажется, что вы неподвижно стоите на карусели, но она вас вращает вокруг своей оси.

Примерно также пространство-время носит любую частицу в ту же сторону, куда вращается массивное тело в центре эргосферы. Вот такое уравнение получил Рой Кер.

Сегодня это, пожалуй, исчерпывает наше представление о том, как выглядит непосредственная окрестность вот этого супермассивного и суперкомпактного тела, которое чуть позже назвали черной дырой.